Examples

Here are a few example illustrating usage of the GEM Library.

Contents

Remarkable numbers

  • Printing the 100 first decimals of $\pi$
disp(gem('pi',100), -1)

  3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170681

Getting a string description of the first 100 decimals of $\pi$

toStrings(gem('pi',100))

ans =

    '3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170681'
  • The number 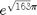$e^{\sqrt{163}\pi}$ is not an integer
f = exp(sqrt(gem(163))*gem('pi'));
display(f, -1)

 
f = 
 
  262537412640768743.999999999999250072597198185688897
 

x = log2(gem(9))
y = gem(2)^0.5
disp(y^x, -1)

 
x = 
 
   3.1699250014423123629
 
 
y = 
 
   1.4142135623730950488
 
  3.00000000000000000000000000000000000000000000000004

(here numerical errors accumulated up to the last two digits)

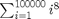
  • A sum of 8th powers: $\sum_{i=1}^{100000} i^8$
e = sum(gem([1:100000]).^8);
disp(e,-1)

  111116111177777777773111111111333333333330000
  • The slowest continued fraction converges to the golden ratio. 118 iterations are needed to recover 50 digits of precision:
x = gem(1);
for i = 1:118
    x = 1/(1+x);
    if mod(i-8,10) == 0
        disp(num2str(1+x,50));
    end
end
disp(num2str((1+sqrt(gem(5)))/2, 50))

1.6181818181818181818181818181818181818181818181818
1.6180339985218033998521803399852180339985218033999
1.6180339887505408393827219845199750012018652949377
1.6180339887498948909091006809994180339887498948909
1.6180339887498948482074099000120490432628425404247
1.6180339887498948482045870209899296988725781961338
1.6180339887498948482045868343779752825511893773124
1.6180339887498948482045868343656389332927878467732
1.6180339887498948482045868343656381177742241981327
1.6180339887498948482045868343656381177203127439638
1.6180339887498948482045868343656381177203091800414
1.6180339887498948482045868343656381177203091798058
1.6180339887498948482045868343656381177203091798058
  • The first few Mersenne prime numbers
p  =  [2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279];
mersennes = gem(2,400).^p-1;
for i = 1:numel(mersennes)
    disp(mersennes(i),-1)
end

  3
 
  7
 
  31
 
  127
 
  8191
 
  131071
 
  524287
 
  2147483647
 
  2305843009213693951
 
  618970019642690137449562111
 
  162259276829213363391578010288127
 
  170141183460469231731687303715884105727
 
  6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057151
 
  531137992816767098689588206552468627329593117727031923199444138200403559860852242739162502265229285668889329486246501015346579337652707239409519978766587351943831270835393219031728127
 
  10407932194664399081925240327364085538615262247266704805319112350403608059673360298012239441732324184842421613954281007791383566248323464908139906605677320762924129509389220345773183349661583550472959420547689811211693677147548478866962501384438260291732348885311160828538416585028255604666224831890918801847068222203140521026698435488732958028878050869736186900714720710555703168729087

Matrix manipulations

  • The sparse identity and its inverse
Id = sgem(speye(3))
inv(Id)

 
Id = 
 
  (1,1)  1
  (2,2)  1
  (3,3)  1
 
 
ans = 
 
  (1,1)  1
  (2,2)  1
  (3,3)  1
  • Computing the few largest eigenvalues of a random matrix
eigs(gem.rand(50,50))

 
ans = 
 
   24.581671408373545504                         
   -2.341875544488036459                         
    1.383987190703709166 +  1.603087135186556046i
    1.383987190703709166 -  1.603087135186556046i
   -0.785113704941533724 -  1.954271046225898242i
   -0.785113704941533724 +  1.954271046225898242i
  • Solving a sparse linear system in high precision
A = sgem([2 4 1 2 2 5 1 3 5 3 4], [1 1 2 2 3 3 4 4 4 5 5], [4 -2 2 -1 -1 4 1 3 2 -6 2]);
b = [8; -1; -18; 8; 20];
x = A\b

 
x = 
 
   1.0000000000000000000
   2.0000000000000000000
   3.0000000000000000000
   4.0000000000000000000
   5.0000000000000000000
 

x1 = sdpvar;
x2 = sdpvar;
options = sdpsettings('solver', 'refiner', 'refiner.internalsolver', 'sedumi');
optimize([7*x2 >= 1 + x1, x1 >= 0], x2, options);

Refiner 1.1 - Iterative meta-solver
 
iter-             iteration    global
ation    time     precision   precision   current value  
---------------------------------------------------------
    1    0.10021  1.7789e-15   6.264e-16  0.142857142857143
    2    0.27635  2.5554e-15   3.354e-27  0.14285714285714285714285714
    3    0.46990  2.0745e-15       1e-38  0.142857142857142857142857142857
---------------------------------------------------------
 
Precision of 1e-38 reached in 3 iterations.

Good to know

  • The default working and display precision
gem.workingPrecision
gem.displayPrecision

ans =

    50


ans =

    20
  • gem and sgem objects can be saved to files
g = 1./gem([1:6]);
save('filename','g');
clean g;
load('filename');
g

loading...done
 
g = 
 
   1.0000000000000000000   0.5000000000000000000   0.3333333333333333333   0.2500000000000000000   0.2000000000000000000   0.1666666666666666667